O Kig suporta a utilização de 'loci'. Um 'loci' é definido matematicamente como o conjunto de todos os pontos ou linhas que satisfazem ou são determinados através de condições específicas; um exemplo é “o 'locus' dos pontos equidistantes de um determinado ponto é uma circunferência”. Vamos ver um exemplo de utilização de 'loci' no Kig:

Considere a seguinte construção geométrica: É desenhada uma circunferência e um ponto que se pode mover ao longo da sua superfície (construa este ponto, posicionando o cursor numa circunferência e clicando com o botão do meio do mouse. Se você então tentar mover o ponto resultante, verá que não consegue movê-lo para fora da circunferência). Depois, é desenhado um segmento desde esse ponto até ao centro da circunferência e o ponto médio desse segmento.

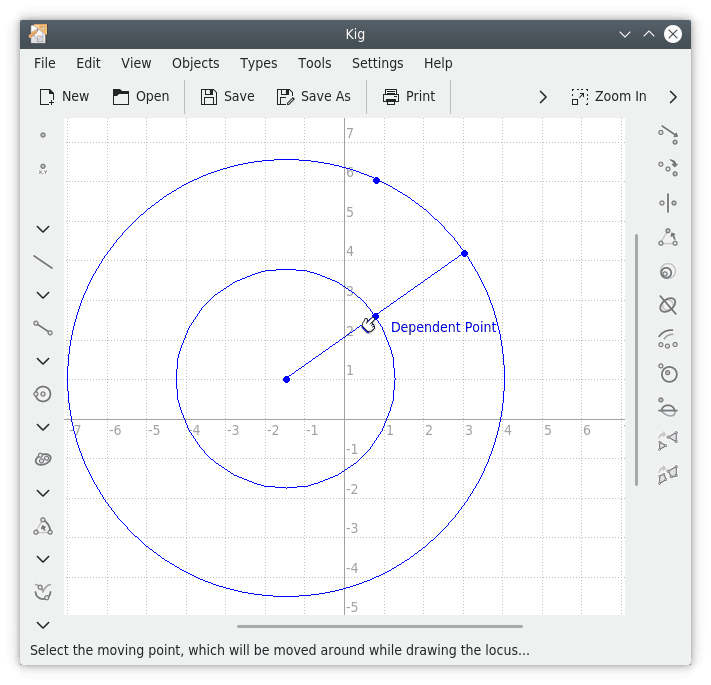
Agora, se mover o ponto que está restringido à circunferência, você poderá ver que o segundo ponto se move com ele. Se você mantivesse uma caneta acima do segundo ponto e movesse o primeiro ponto à volta da circunferência, iria criar uma nova circunferência com metade do tamanho da outra. Veremos abaixo que isto é exatamente o que um 'locus' faz. O caminho que o segundo ponto percorre enquanto o primeiro se move à volta da circunferência é como ficaria o 'locus'.

De fato, a criação do 'locus' é muito simples. Clique no seu botão na barra de ferramentas ou selecione a opção Objetos → Outros → 'Locus' do menu. Selecione então o ponto restrito como o ponto móvel (o texto Ponto Móvel irá aparecer à medida que você passa o mouse por cima) e o outro como ponto dependente. Irá então aparecer o 'locus'.