Índice
O KmPlot lida com vários tipos diferentes de funções, os quais poderão ser gravados na forma de funções ou de equações:
Os gráficos cartesianos poderão ser gravados como isto é “y = x^2”, onde o 'x' terá de ser usado como variável ou como isto é “f(a) = a^2”, onde o nome da variável é arbitrário.
Os gráficos paramétricos são semelhantes aos gráficos Cartesianos. As coordenadas 'x' e 'y' poderão ser introduzidas como equações em ordem a 't', isto é “x = sin(t)”, “y = cos(t)” ou como funções, isto é “f_x(s) = sin(s)”, “f_y(s) = cos(s)”.
Os gráficos polares são também semelhantes aos gráficos Cartesianos. Estes poderão tanto ser indicados como uma equação em ordem a θ, isto é “r = θ”, ou como uma função, p.ex. “f(x) = x”.
Para os gráficos implícitos, o nome da função é indicado em separado da expressão que relaciona as coordenadas 'x' e 'y'. Se as variáveis 'x' e 'y' forem indicadas através do nome da função (escrevendo isto é“f(a,b)” como o nome da função), então estas variáveis serão usadas. Caso contrário, as letras 'x' e 'y' serão usadas para as variáveis.
Os gráficos diferenciais explícitos são equações diferenciais, onde a derivada maior é indicada em função das derivadas menores. A derivação é indicada através de uma plica ('). No formato da função, a equação ficará algo do tipo “f''(x) = f' − f”. No formato de equação, ficará algo do tipo “y'' = y' − y”. Repare que, em ambos os casos, a parte “(x)” não é adicionada aos termos diferenciais de menor ordem (pelo que poderia indicar “f'(x) = −f” mas não “f'(x) = −f(x)”).
Todos os campos de texto da equação vêm com um botão à direita. Se carregar neste, irá invocar a janela do Editor de Equações avançado, que oferece:
Uma variedade de símbolos matemáticos que poderão ser usados nas equações, mas que não existem nos teclados normais.
A lista das constantes do utilizador e um botão para as editar.
A lista de funções predefinidas. Lembre-se que, se tiver algum texto já seleccionado, este será usado como argumento da função, quando for introduzida uma função. Por exemplo, se tiver seleccionado “1 + x” na equação “y = 1 + x”, e for seleccionada a função seno, a equação irá ficar igual a “ y = sin(1+x)”.
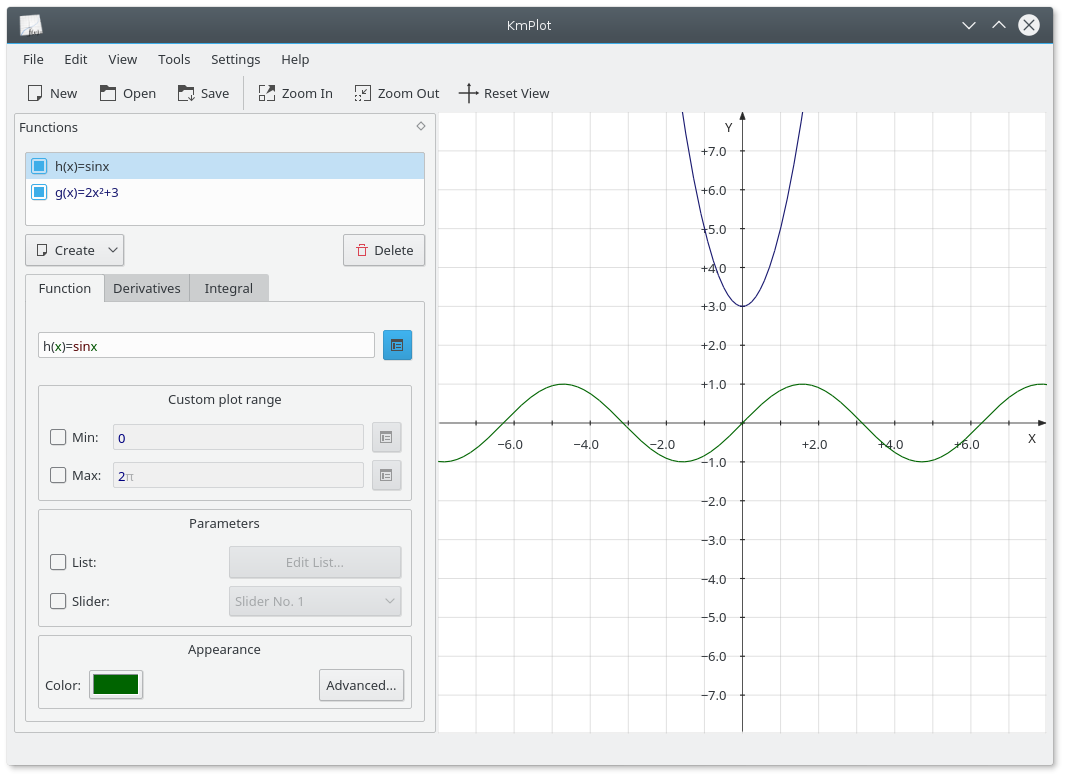
Para introduzir uma função explícita (isto é, uma função no formato y=f(x)) no KmPlot, basta indicá-la no formato seguinte:
f(x) = expressãoEm que:
O
fé o nome da função, e poderá ser qualquer sequência de letras e números que desejar.O
xé a coordenada horizontal, que pode ser usada na expressão que se segue ao sinal de igualdade. É de facto uma variável inútil, por isso você poderá usar qualquer nome de variável que desejar para obter o mesmo efeito.A
expressãoé a fórmula propriamente dita a ser desenhada, usando uma sintaxe apropriada para o KmPlot. Veja a “Sintaxe Matemática”.
As funções paramétricas são aquelas em que as coordenadas 'x' e 'y' são definidas por funções separadas de outra variável, normalmente chamada de 't'. Para indicar uma função paramétrica no KmPlot, siga o procedimento usado para uma função cartesiana, mas defina antes o nome da função que descreve a coordenada X com a letra 'x', e a função que descreve a coordenada 'y' com a letra 'y'. Tal como acontece nas funções cartesianas, você poderá usar qualquer nome de variável que desejar como parâmetro.
Como exemplo, suponha que deseja desenhar uma circunferência, que tem as equações paramétricas 'x = sin(t)', 'y = cos(t)'. Depois de criar um gráfico paramétrico, indique as equações apropriadas nos campos 'x' e 'y', isto é, f_x(t) = sin(t) e f_y(t) = cos(t).
Você poderá definir mais algumas opções para o gráfico no editor de funções:
- Mín, Máx
Estas opções controlam o intervalo do parâmetro 't', para o qual está desenhada a função.
As coordenadas polares representam um ponto pela sua distância à origem (normalmente chamada de 'r'), e pelo ângulo que é feito por uma linha desde a origem até ao ponto em relação ao eixo dos X (normalmente representado pela letra grega 'theta' - θ). Para indicar as funções em coordenadas polares, carregue no botão Criar e seleccione Gráfico Polar na lista. No campo de definição, termine a definição da função, incluindo o nome da variável 'theta' que deseja usar; isto é, para desenhar a espiral de Arquimedes, r=θ, indique:
r(θ)=θ, para que a linha inteira seja “r(t)=t”. Lembre-se que você poderá usar qualquer nome para a variável 'theta', por isso, o “f(x)=x” teria dado exactamente o mesmo resultado.
Uma expressão implícita relaciona as coordenadas 'x' e 'y' como uma igualdade. Para criar uma circunferência, por exemplo, crie um Gráfico Implícito novo no botão Criar e Gráfico Implícito. Depois, indique no campo da equação (por baixo do campo do nome da função) o seguinte:
x^2 + y^2 = 25
O KmPlot consegue desenhar equações diferenciais explícitas. Estas são equações no formato y(n) = F(x,y',y'',...,y(n−1)), onde o yk é a késima derivada de y(x). O KmPlot só consegue derivar a ordem da derivada como o número de plicas a seguir ao nome da função. Para desenhar uma curva sinusoidal, por exemplo, iria usar a equação diferencial y'' = − y ou f''(x) = -f.
Contudo, uma equação diferencial, por si só, não é suficiente para determinar um gráfico. Cada curva do diagrama é gerada através da combinação das equações diferenciais e das condições iniciais. O utilizador poderá editar as condições iniciais, se carregar na página Condições Iniciais, quando seleccionar uma equação diferencial. O número de colunas oferecido para editar as condições iniciais depende da ordem da equação diferencial.
Você poderá definir mais algumas opções para o gráfico no editor de funções:
- Passo
O valor do passo, no campo de precisão, é usado para resolver numericamente a equação diferencial (usando o método de Range Kutta). O seu valor é o tamanho máximo do passo usado; um valor menor do passo poderá ser usado se parte do gráfico diferencial estiver ampliada a um valor próximo o suficiente.