Inhaltsverzeichnis
In KmPlot können Sie mit unterschiedliche Arten von Funktionen benutzen, dabei können Sie sie als Funktion oder als Ausdruck eingeben.
Kartesische Funktionen können Sie entweder als z. B. „y = x^2“, dabei muss x als Name der Variable benutzt werden, oder als z. B. „f(a) = a^2“ eingeben, dabei können Sie einen beliebigen Namen für die Variable verwenden.
In parametrischen Funktionen werden die x- und y-Koordinaten als Ausdrücke von t, z. B. „x = sin(t)“, „y = cos(t)“ oder als Funktionen wie z. B. „f_x(s) = sin(s)“, „f_y(s) = cos(s)“ eingegeben.
Polare Funktionen können entweder als Ausdrücke von θ, z. B. „r = θ“ oder als Funktionen wie z. B. „f(x) = x“ eingegeben werden.
Bei impliziten Funktionen kann der Name der Funktion getrennt von dem Ausdruck für die x- und y-Koordinaten eingegeben werden. Wenn die Variablen x und y über den Funktionsnamen festgelegt werden (z. B. mit „f(a,b)“ als Name der Funktion), dann werden diese Variablen a und b verwendet. Ansonsten werden die Buchstaben x und y für die Variablen benutzt.
Explizite Differentialfunktionen werden durch Differentialgleichungen beschrieben, in denen die höchste Ableitung als Ausdruck der niedrigeren Ableitungen angegeben wird. Die Ableitung wird durch das Zeichen ' gekennzeichnet. Als Funktionsform lautet die Gleichung zum Beispiel „f''(x) = f' − f“, als Gleichungsform „y'' = y' − y“. In beiden Fällen wird „(x)“ nicht in den niedrigeren Ableitungen eingefügt. Die richtige Schreibweise ist also „f'(x) = −f“ und nicht „f'(x) = −f(x)“).
Die Eingabefelder der Funktionen haben rechts einen Knopf. Damit öffnen Sie den Gleichungseditor, der folgende Funktionen bietet:
Eingabe vieler mathematischer Symbole, die nicht auf der normalen Tastatur vorhanden sind, in Funktionsgleichungen.
Eingabe benutzerdefinierter Konstanten und die Möglichkeit zur Bearbeitung dieser Konstanten.
Eine Liste vordefinierter Funktionen. Wenn Sie bereits Text markiert haben, wird dieser Text als Argument benutzt, wenn Sie eine Funktion einfügen. Ist zum Beispiel „1 + x“ in der Gleichung „y = 1 + x“ markiert und Sie wählen die Sinusfunktion, erstellen Sie damit die Gleichung „ y = sin(1+x)“.
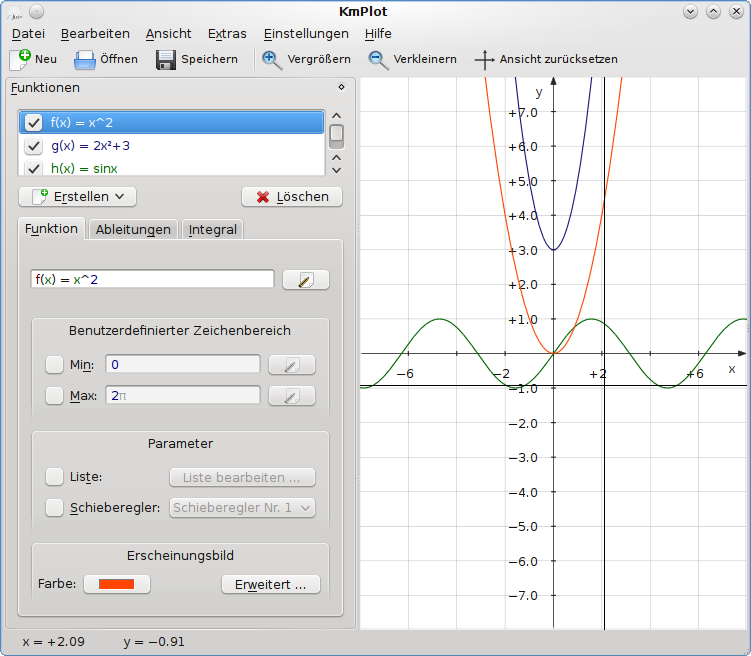
Eine explizite Funktion (d. h. eine Funktion in der Form y=f(x)), können Sie in KmPlot auf folgende Art eingeben:
f(x)=AusdruckDabei ist:
fder Name der Funktion und kann aus jeder Kombination von Buchstaben und Zahlen bestehen.xdie waagerechte Koordinate, die im Ausdruck benutzt wird, der nach dem Gleichheitszeichen folgt. Das ist ein Platzhalter, also können Sie jeden beliebigen Namen verwenden, das Ergebnis ist das Gleiche.Ausdruckist der Ausdruck, der gezeichnet werden soll, in der von KmPlot geforderten Schreibweise. Siehe dazu „Mathematische Syntax“.
In parametrischen Funktionen werden die x- und y-Koordinaten über unabhängige Funktionen einer anderen Variable, oft t genannt, definiert. Um eine parametrische Funktion in KmPlot zu zeichnen, geben Sie die x- und y-Funktion als kartesische Funktionen ein. Auch hier können Sie einen beliebigen Variablennamen für die Parameter verwenden.
Angenommen, Sie möchten eine Kreis mit dem parametrischen Ausdruck x = sin(t), y = cos(t) zeichnen. Wählen Sie dazu Parametrische Zeichnung und geben Sie die passenden Ausdrücke in das x- und y-Eingabefeld ein, d. h. f_x(t)=sin(t) and f_y(t)=cos(t).
Sie können noch weitere Optionen für die Zeichnung im Funktionen-Editor einstellen:
- Min:, Max:
Diese Einstellungen geben den Wertebereich des Parameters t an, für den die Funktion gezeichnet wird.
Polarkoordinaten bestimmen einen Punkt durch den Abstand vom Ursprung (üblicherweise r genannt) und durch den Winkel einer Linie vom Ursprung durch den Punkt zur waagerechten Achse (üblicherweise mit dem griechischen Buchstaben θ bezeichnet). Funktionen in polaren Koordinaten erzeugen Sie, indem Sie auf klicken und Polare Zeichnung wählen. Im Eingabefeld geben Sie die Definition der Funktion mit dem Namen der theta-Variablen ein. Um z. B. die Spirale des Archimedes r = θ zu zeichnen, geben Sie ein:
r(θ) = θ. Sie können jeden beliebigen Namen als theta-Variable verwenden, daher ergibt „r(t) = t“ oder „f(x) = x“ die gleiche Zeichnung.
Ein impliziter Ausdruck gibt die Beziehung zwischen x- und y-Koordinaten als Gleichung an. Um zum Beispiel einen Kreis zu zeichnen, klicken Sie auf den Knopf und wählen Implizite Zeichnung aus der Liste. Tragen Sie dann im Gleichungsfeld unter dem Funktionsnamen folgendes ein:
x^2 + y^2 = 25
KmPlot kann explizite Differentialgleichungen darstellen. Dies sind Gleichungen in der Form y(n) = F(x,y',y'',...,y(n−1)), dabei ist yn die n-te Ableitung von y(x). Die Ordnung der Ableitung wird aus der Anzahl der ' nach der Funktionsbezeichnung bestimmt. Um zum Beispiel eine sinusförmige Kurve zu zeichnen, geben Sie als Differentialgleichung y'' = − y oder f''(x) = −f ein.
Jedoch nur die Differentialgleichung allein ist noch nicht ausreichend für die Erstellung der Zeichnung. Jede Kurve im Diagramm wird durch die Differentialgleichung und die Startbedingung festgelegt. Wenn eine Differentialgleichung ausgewählt ist, können Sie die Startbedingung auf der gleichnamigen Karteikarte eingeben. Die Anzahl der Spalten für die Eingabe der Startbedingungen wird durch die Ordnung der Differentialgleichung bestimmt.
Sie können noch weitere Optionen für die Zeichnung im Funktionen-Editor einstellen:
- Schritt:
Die Schrittweite im Feld Genauigkeit wird zur numerischen Lösung der Differentialgleichung mit der Runge-Kutta-Methode benutzt. Der Wert bestimmt die maximale Schrittweite, bei Vergrößerung der Zeichnung wird mit einer kleineren Schrittweite gerechnet.